Question

Brianna bought her car for $35,543. It is expected to depreciate an average of 19%each year during the first 10 years.What will the approximate value of her car be in 10 years? Round answer to thenearest dollar.

Answer 1

Percentage increase or decrease

Let's assume we have a certain quantity V that increases or decreases over time at a rate of p% over t units of time (t can be hours, days, months, years, etc). The value V'(t) after t units of time is then given by:

`V^(\prime)(t)=V\cdot(1\pm(p)/(100))^t`

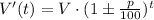
Where we use the + sign if we are talking about an increasing and the - sign if we are talking about a decreasing.

Brianna's car

We are told that Brianna's car was bought by $35543. We know that it decreases at a rate of 19% per year which means that p=19 and the price of Brianna's car after t years is given by:

`\begin{gathered} V^(\prime)(t)=35543\cdot(1-(19)/(100))^t \\ V^(\prime)(t)=35543\cdot0.81^t \end{gathered}`

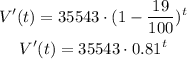
Then the approximate value of the car in 10 years is V'(10):

`V^(\prime)(10)=35543\cdot0.81^(10)=4321.199`

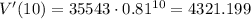
Then the answer is $4321.