First, let's calculate the probability of winning the game.
We win the game if we get three heads or three tails, so the probability is:
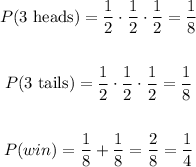
If the probability of winning is 1/4, the probability of losing is 3/4.
If the wager is $1, winning will return $4 plus the original bet, so a net earning of $4.
Losing will return nothing, so the net "earning" is -$1.
Calculating the expected value of one game, we have:
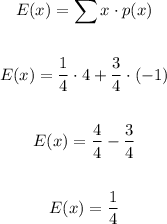
Playing 20 times will result in an earning of 20 * 1/4, that is, a gain of $5.
Correct option: fourth one.