We can answer this question as follows:
1. We have two consecutive integers, and we can express them as follows:
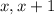
2. We need the product of them to be equal to 812:
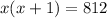
3. Now, we can expand the product as follows - we can apply the distributive property:
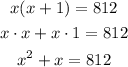
4. We can subtract 812 from both sides of the equation, and we end up with a quadratic equation:
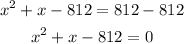
5. We have to apply the quadratic formula to solve this equation as follows:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a},ax^2+bx+c=0](https://img.qammunity.org/2023/formulas/mathematics/college/d8qkmmh3mxtoovm8j5ja34n7ks11xlfyof.png)
And we have that:
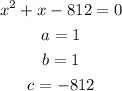
6. Now, we can apply the quadratic formula:
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-1\pm\sqrt[]{(1)^2-4(1)(-812)_{}}}{2(1)} \\ x=\frac{-1\pm\sqrt[]{1^{}+3248_{}}}{2(1)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wygs2p2rkneya0xq5vszk22rt3k1c62zmi.png)
Then we can continue to finally have two solutions:
![\begin{gathered} x=\frac{-1\pm\sqrt[]{3249_{}}}{2(1)} \\ x=(-1\pm57)/(2) \\ x_1=(-1+57)/(2)=(56)/(2)\Rightarrow x_1=28 \\ x_2=(-1-57)/(2)=(-58)/(2)\Rightarrow x_2=-29 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9hafz1vfj3v0elzf09o51t7aax1yxbbwqo.png)
7. We can, now, check which of the two solutions are the correct one:
If we check with x = 28, we have:
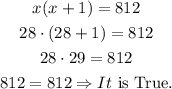
If we check with x = -29, we have:

Therefore, we have two possible answers:
• 28 and 29
,
• -29 and -28
They are integers (one pair positive, and the other pair negative integers).
In summary, then we can say:
For 28 and 29:
• The smallest integer is 28
,
• The largest integer is 29
For -29 and -28
• The smallest integer is -29
,
• The largest integer is -28
[We need to remember that integers are all "positive and negative whole numbers: {..., -3, -2, -1, 0, 1, 2, 3, 4, 5, ...}.] {...