From the figure, we can deduce the following:
Diameter of the cylinder = 7⅕ ft.
Height of the cylinder = x ft
Here, the surface area of the cylinder is equal to the value of the volume of the cylinder.
Let's solve for x.
Formula for Volume of a cylinder:
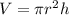
Formula for Surface area of a cylinder:
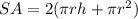
Since the values for both surface area and volume are equal, equate both formula:
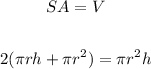
Let's simplify the equation.
Divide through by πr:
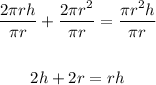
Write the equation for h.
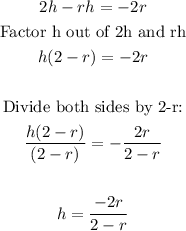
Where:
h is the height
r is the radius.
To find the radius, we have:
radius = diameter/2 = 7.2/2 = 3.6 ft
Now, to find the height, substitute 3.6 for r and evaluate:
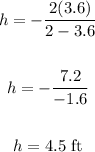
Therefore, the height of the cylinder, is 4.5 ft.
x = 4.5
Let's find the surface area:
Where:
r = 3.6 ft
h = 4.5 ft
We have:
![undefined]()