Question

Factor completelyor state that the polynomial is prime.x^3 - 5x^2 - 16x + 80

Answer 1

1) Let's start by grouping this polynomial

`\begin{gathered} x^3-5x^2-16x+80 \\ (x^3-5x^2)\text{ }+(-16x+80) \end{gathered}`

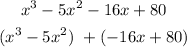
2) Now, let's find the GCD from x³, 5x² and on the second parentheses, 16,80 and write it as a factor, placing the GCD of each group outside the parentheses:

GCD x³, 5x² = x² and the GCD of 16, 80 = 16

`\begin{gathered} (x^3-5x^2)\text{ }+(-16x+80) \\ x^2(x-5)\text{ +}16(x\text{ -5)} \end{gathered}`

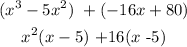
3) As we can see there is a repetition, of terms let's rewrite it this way and factorize x²-16 reminding that a²-b² = (a+b)(a-b)

`\begin{gathered} x^2(x-5)\text{ -}16(x\text{ -5)} \\ (x-5)(x+4)(x-4) \end{gathered}`

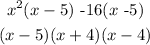
So x³-5x²-16x +80 factored into its simplest form is (x-5)(x+4)(x-4)