Question

Find the equation of the parabola with vertex (5, -3) that passes throughthe point (2, 33).

Answer 1

Given:

The vertex of a parabola is (h, k) = (5, -3).

The parabola passes through the point (x, y) = (2,33).

The objective is to find the equation of the parabola.

Step-by-step explanation:

The general equation of parabola is,

`y=a(x-h)^2+k\text{ . . . .(1)}`

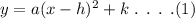
To find a :

On plugging the given values of (h, k) and (x,y) in equation (1),

`33=a(2-5)^2+(-3)`

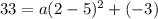
On further solving the above equation,

`\begin{gathered} a(-3)^2=33+3 \\ a=(36)/(9) \\ a=4 \end{gathered}`

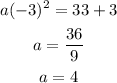
To find the equation of parabola:

Now, substitute the value of a and (h, k) in equation (1).

`y=4(x-5)^2+(-3)`

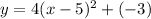
On further solving the above equation,

`\begin{gathered} y=4(x^2-2(x)(5)+5^2)-3 \\ =4(x^2-10x+25)-3 \\ =4x^2-40x+100-3 \\ =4x^2-40x+97 \end{gathered}`

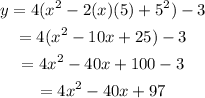
Hence, the equation for parabola is y = 4x²-40x+97.