Question

a school group sells gift cards and gift wrap for a fund raiser. 20 cards and 40 gift wraps sell for 160 dollars. 10 cards and 30 gift wrap sell for 110 dollars. How much does each gift wrap cost?

Answer 1

The cost of each gift wraps g = $3

Let us make the price of one card = c.

Let us make the price of one gift wrap = g.

Now we can create equations from the statements made in the question:

20 cards and 40 gift wraps sell for $160

Meaning:

`20c+40g=160`

Let this equation be called equation 1.

Next, we analyze the next part of the question which says:

10 cards and 30 gift wraps sell for $110

Meaning:

`10c+30g=110`

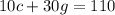
Let this be called equation 2.

Let us multiply the second equation by 2

`\begin{gathered} 2*(10c+30g=110) \\ 20c+60g=220 \end{gathered}`

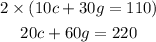
Let this new equation be called equation 3.

We multiplied out equation 2 by 2 because we wanted at least one of the equation coefficients to be the same.

Now we can subtract equation 3 and equation 1.

`\begin{gathered} \text{equation 1:} \\ 20c+40g=160 \\ \text{equation 3:} \\ 20c+60g=220 \\ \\ \text{Subtracting both equation} \\ 20c+40g=160 \\ -(20c+60g)=220 \\ =20c-20c+40g-60g=160-220 \\ -20g=-60 \\ \text{divide both sides by -20} \\ \\ g=-(60)/(-20)=3 \end{gathered}`

The cost of each gift wraps g = $3