Using the given information, we have the points (5.5, 60) and (8, 150). Let's find the ratio-
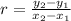
Where
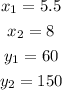
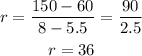
This ratio represents the slope of the linear equation.
Then, we use the point-slope formula to find the equation that models this situation

The correct equation is the third option.
Now, we can find the number of pulls after 30 minutes using the equation
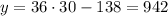
The number of pull-ups after 30 minutes is 942.