Question

Scale homework help

Answer 1

In the triangle USI

US = 26+13

US=39

SI=39

IU=x

In triangle WSH

WS=26

SH=26

WH=20

Thus, we get :

`(WS)/(SU)=(HS)/(SI)=(26)/(39)`

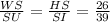
Ratio of the two sides of triangle are same and the angle S is common

So, by SAS Similarity

Triangle USI and triangle WSh are similar

From the properties of similar triangle, the ratio of corresponding sides of triangle are always similar

So,

`\begin{gathered} (SW)/(SU)=(SH)/(SI)=(HW)/(IU) \\ \text{Substitute the values} \\ (26)/(39)=(26)/(39)=(20)/(x) \\ \text{Simplify the last two} \\ (26)/(39)=(20)/(x) \\ x=(20*39)/(26) \\ x=30 \end{gathered}`

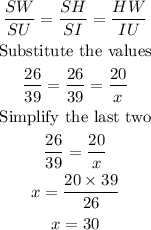
Answer: x = 30