Answer:
(4,5)
Step-by-step explanation:
Given the system of equations:
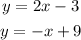
We graph each of the equation using the x and y-intercepts.
First Equation(y=2x-3)
When x=0
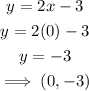
When y=0
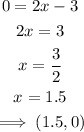
Next, join the points (0,-3) and (1.5,0) as shown below:
Second Equation(y=-x+9)
When x=0
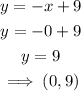
When y=0
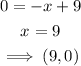
Next, join the points (0,9) and (9,0) on the same graph as shown below:
The point where the two lines intersect is the solution to the system of equations.
Therefore, the solution is (4,5).