Question

What the answer to this problem f(x)=-4x^2+12x-9find the zeros of the function

Answer 1

You have the following function:

`f(x)=-4x^2+12x-9`

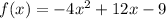
In order to determine the zeros of the function, use the quadratic formula, given by:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where a, b and c are coeeficients of the function f(x). In this case the value of these coefficients are:

a = -4

b = 12

c = -9

By replacing the previous values into the quadratic formula and by simplifying you obtain:

`\begin{gathered} x=\frac{-12\pm\sqrt[]{(12)^2-4(-4)(-9)}}{2(-4)} \\ x=\frac{-12\pm\sqrt[]{144-144}}{-8} \\ x=(-12)/(-8)=(3)/(2) \end{gathered}`

Hence, there is one zero for the given function at x=3/2