The linear function that the any variables have the highest degree of 1
A linear function have two, three five.. infinity number of variables.
for eg :

The expression for the linear function is :
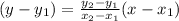
Here we have y = f(x)
5) f(-2)= -3 & f(0)=5
Here, we have x =-2, and y=-3
x=0 and y =5
So, the equation

Answer : Required equation : y = 4x+5
6) f(-2)=4 & f(-5)=7
Here we have at x =-2 and f(-2)=4 i.e y = 4
and at x = -5 and f(-5) =7i.e y =7
So, the equation is :
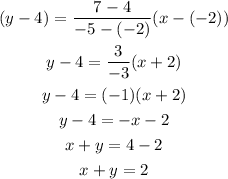
Answer : Required Equation : x + y =2