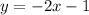We can see the graph of a line, and we have the following points: (0, -1) and (1, -3), and we need to find the equation of the line in slope-intercept form.
Then to find the equation, we can proceed as follows:
1. We have to apply the two-point equation of the line:
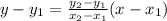
2. Now, we can label both points as follows:
• (0, -1) ---> x1 = 0, y1 = -1
,
• (1, -3) ---> x2 = 1, y2 = -3
3. We can substitute these values into the two-point form of the line:
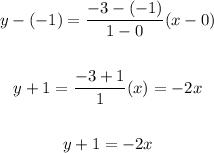
4. Finally, we have to subtract 1 from both sides of the equation:
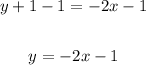
Therefore, in summary, the equation of the line in slope-intercept form is: