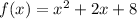Given the functions:
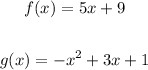
Where f(x) is the amount of energy the microwave uses and g(x) is the amount of energy it puts out.
Let's find the difference between the amount of energy the microwave uses and the amount it puts out.
To find this difference, we have:
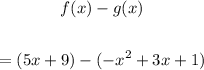
Apply distributive property and remove the parentheses:
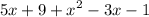
Combine like terms and reorder the expressions:
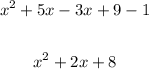
Therefore, the difference between the amount of energy the microwave uses and the amount it puts out is:
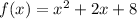
ANSWER: