Question

Question 11. For the balanced equation shown below, howmany grams of CO will be produced, if 1380grams of Cl, are produced?4C2HCI+902=>8C0+10H2O+2Cl22. For the balanced equation shown below, how many moles of so, will be produced by1.09moles of SO,?2502+O2=>25033. For the unbalanced equation shown below, howmany moles of LizN reacted, if 3.65 grams of Liare produced?LizN=>Li+N24. Nitrogen gas and hydrogen gas are combined toform ammonia. What mass of ammonia can beproduced from a 10.00 gram sample of nitrogenis combined with an excess of oxygen.(N,+H2 →NH3)

Answer 1

Answer: the mass of CO produced is 2.181 x 10^3 g

Step-by-step explanation:

The question requires us to calculate the amount of CO, in grams, that would be obtained in the reaction given, considering that 1380 g of Cl2 were produced.

The following chemical equation was provided by the question:

`4C_2HCI+9O_2\rightarrow8CO+10H_2O+2Cl_2`

Note that the chemical equation is not properly balanced (there are 4 H atoms on the left side and 20 H atoms on the right side).The balanced chemical equation is as it follows:

From the balanced chemical equation shown above, we can see that when 2 moles of Cl2 are produced, 8 moles of CO are produced. Thus, to solve this problem, we must calculate how many moles of Cl2 were obtained (considering the mass given, 1380 g), and then relate this amount with the stoichiometry of the reaction.

We can calculate the number of moles of a substance considering the following equation:

`number\text{ of moles \lparen mol\rparen = }\frac{mass\text{ \lparen g\rparen}}{molar\text{ mass \lparen g/mol\rparen}}\rightarrow n=(m)/(M)`

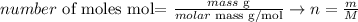
The molar mass of Cl2 is 70.91 g/mol and the mass of this substance that was produced is 1380 g:

`n=(m)/(M)=(1380g)/(70.91g/mol)=19.46mol`

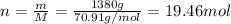
Therefore, 19.46 moles of Cl2 were obtained.

Considering the stoichiometry of the reaction, given by the balanced chemical equation, we can write:

2 mol Cl2 -------------------------- 8 mol CO

19.46 mol Cl2 -------------------- x

Solving for x, we'll have:

`x=\frac{(19.46mol\text{ C}l_2)*(8mol\text{ CO\rparen}}{(2mol\text{ C}l_2)}=77.84mol\text{ CO}`

Therefore, 77.84 moles of CO were obtained in this reaction.

We can convert this amount of moles of CO to its correspondent mass, in grams, using the following equation:

`n=(m)/(M)\rightarrow m=n* M`

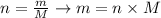
The molar mass of CO is 28.01 g/mol, thus its mass will be:

`m=n* M=77.84mol*28.01g/mol=2.181*10^3g`

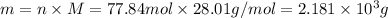
Therefore, the mass of CO produced is 2.181 x 10^3 g.