Question

Ethan invests $9100 In two different accounts. the first account paid 4%, the second account paid 11% in interest. at the end of the first year he had earn $763 in interest. how much was in each account?

Answer 1

Consider the following formula for the simple intereset:

`I=P\cdot r\cdot t`

where

P: principal investment

r: interest rate

t: time

In this case, you have two diferent interest I1 and I2, and its principals P1 and P2.

Take into account that P1 = 9100 - P2, and r1 = 0.04 and r2 = 0.11.

Furthermore, consider that I2 = 763 - I1.

Replace the previous values of the parameters into the expression for I1 and I2:

`\begin{gathered} I_1=P_1\cdot r\cdot t \\ I_1=\mleft(9100-P_2\mright)\mleft(0.04\mright)\mleft(1\mright) \\ I_1=364-0.04P_2 \\ \\ I_2=P_2\cdot r\cdot t \\ 763-I_1=P_2(0.11)(1) \\ -I_1=0.11P_2-763 \end{gathered}`

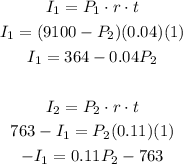
Then, you have a system of equations for I1 and P2. In order to solve it, proceed as follow:

Add both equations and solve for P2:

I1 = -0.04P2 + 364

-I1 = 0.11P2 - 763

0 = 0.07P2 - 399

0.07P2 = 399

P2 = 399/0.07

P2 = 5700

Next, use the previous result to find P1:

P1 = 9100 - 5700

P1 = 3400

Then, find the interest earnt on each account:

I1 = 3400*0.04*1 = 136

I2 = 5700*0.11*1 = 627