Given the line segment CD, point E divides CD three-fourths of the way from C to D
If you graph segment CD and divide it in four, count starting from C three cuarters and you'll get the location of point E
To calculate the coordinates of E, first you have to determine the distance between points C and D.
C (1,6) D (-3, -4)
Distance over the x-axis:
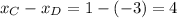
Multiply it by 3/4
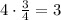
The x-coordinate of Point E
Subtract the calculated distance to the x-coordinate of point C
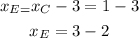
Distance over the y-axis:
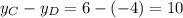
Multiply it by 3/4 to determine the distance of E over the y-axis
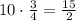
Subtract it to the y-coordinate of C to determine the coordinate of E
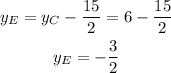
Point E is in coordinates (-2,-3/2)