Question

Given directed line segment CD, if point E divides CD three-fourths of the way from C to D. find the coordinates of E. then plot E.C (1,6) D (-3, -4)

Answer 1

Given the line segment CD, point E divides CD three-fourths of the way from C to D

If you graph segment CD and divide it in four, count starting from C three cuarters and you'll get the location of point E

To calculate the coordinates of E, first you have to determine the distance between points C and D.

C (1,6) D (-3, -4)

Distance over the x-axis:

`x_C-x_D=1-(-3)=4`

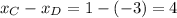
Multiply it by 3/4

`4\cdot(3)/(4)=3`

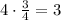
The x-coordinate of Point E

Subtract the calculated distance to the x-coordinate of point C

`\begin{gathered} x_(E=)x_C-3=1-3 \\ x_E=3-2 \end{gathered}`

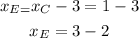
Distance over the y-axis:

`y_C-y_D=6-(-4)=10`

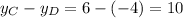
Multiply it by 3/4 to determine the distance of E over the y-axis

`10\cdot(3)/(4)=(15)/(2)`

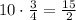
Subtract it to the y-coordinate of C to determine the coordinate of E

`\begin{gathered} y_E=y_C-(15)/(2)=6-(15)/(2) \\ y_E=-(3)/(2) \end{gathered}`

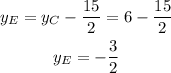
Point E is in coordinates (-2,-3/2)