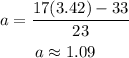Given,
The linear equations are,
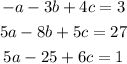
Taking equation first as,
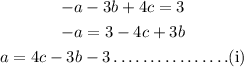
Substituting the value of a from equation (i) to equation second,
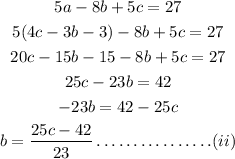
Subsituting the value of b in equation (i),
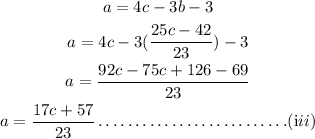
Subsituting the value of a from equation (iii) to last equation,
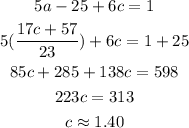
Suubstituting the value of c in equation (ii),
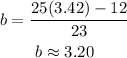
Subsituting the value of c in equation (iii),