Question

John swam 8 kilometers against the current in the same amount of time it took him to swim 16 kilometers with the current. The rate of the current was 1 kilometer per hr. How fast would John swim if there were no current?

Answer 1

Let's call John's speed J.

Let's recall that speed is distance/time. Since the current was 1 km per hour, we can consider this as a subtraction when he was swiming against the current, and as an addition when he was swiming with it.

Since speed is distance/time, time is distance/speed.

This gives us, on one hand,

`t=(8)/(J-1),`

and on the other,

`t=(16)/(J+1)\text{.}`

The problem is telling us that these times are the same, so we get the following equation:

`(8)/(J-1)=(16)/(J+1)\text{.}`

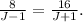
To solve it, let's multiply both sides by (J-1)(J+1):

`(J+1)8=(J-1)16,`
`8J+8=16J-16.`

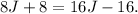
Let's subtract 8 from both sides:

`8J=16J-24.`

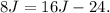
Now, let's subtract 16J from both sides:

`-8J=-24.`

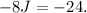
Dividing both sides by -8:

`J=3.`

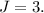
So Jhon would swim at a speed of 3 km/h if there were no current.