Since the weight and fuel have a linear relation, we can write it as

where y denotes the weight in pounds and x the fuel in gallons.
We have 2 points of this linear relation, they are
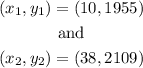
so the slope m from above is given as
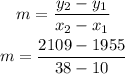
which gives
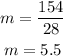
Then, the line equation has the form
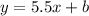
Now, we can find the y-intercept b by replacing one of the two given points, that is, if we substitute point (10,1955) into the last result, we get
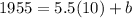
then, b is obtained as
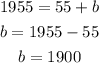
So, the line equation which model this problem is
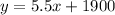
Hence, by using this equation, we can find the weight of the airplane when the fuel is equal to 56 gallons, that is,
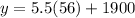
which gives
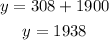
How much does the airplane weight if it’s carrying 56 gallons of fuel? 1938 pounds