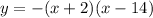In the given graph, the coordinates of the vertex of the parabola is,
(h, k)=(6, 64)
The given parabola is open downwards.
The vertex form of a parabola openingupwards or downwards is given by,
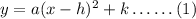
Here, a is a constant and (h, k) are the coordinates of the vertex of the parabola.
If a>0, parabola opens upwards and if a<0, theparabola opens downwards.
(x,y)=(14,0) is a point on the given parabola. So, put x=14, y=0 h=6 and k=64 in the above equation to find the value of a.
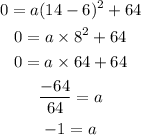
Now, put the values of a, h and k in equation (1).
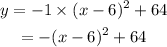
Now, rewriting the above equation,
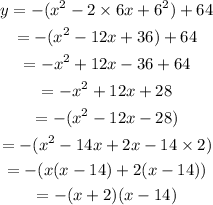
Therefore, the equation of parabola is,