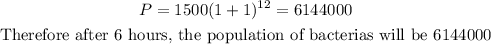Notice that the size of the population of bacteria can be model as an exponential function, meaning:
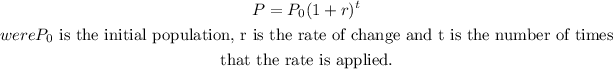
Substituting P₀=1500, r=1, and t=80/30 we get:
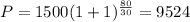
Therefore after 80 minutes, the population of bacterias will be 9524.
For the second question, substituting P₀=1500, r=1, and t=12 we get: