Question

An advertisement consists of a rectangular printed region plus 3-cm margins on the sides and 5-cmmargins at top and bottom. If the area of the printed region is to be 162 cm², find the dimensions of theprinted region that minimize the total area.Printed region: l=w=

Answer 1

Given:

An advertisement consists of a rectangular printed region plus 3-cm margins on the sides and 5-cm

margins at top and bottom.

The area of the printed region is to be 162 cm².

Required:

To find the dimensions of the printed region that minimize the total area.

Step-by-step explanation:

Let the length and width of the printed region be l and w.

Then it is given that the printed area

`A1=lw`

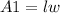
So

`\begin{gathered} lw=162cm^2 \\ \\ l=162w^(-1) \end{gathered}`

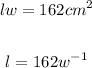
Now, the total length is (l+10) cm and the total width is (w+6) cm.

So the total area A is

`\begin{gathered} A=(l+10)(w+6) \\ \\ A=(162w^(-1)+10)(w+6) \\ \\ A=162+972w^(-1)+10w+60 \\ \\ A=222+972w^(-1)+10w \end{gathered}`

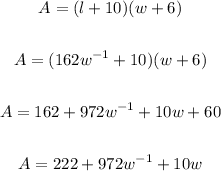
To find the maximum area, we find the extreme points of A by differentiating A with respect to w and setting the resulting derivative to zero. So,

`(dA)/(dw)=-972w^(-2)+10`
`\begin{gathered} 0=972w^(-2)+10 \\ \\ 972w^(-2)=10 \\ \\ 972=10w^2 \\ \\ w^2=(972)/(10) \\ \\ w^2=97.2 \\ \\ w=√(97.2) \\ \\ w=9.8590cm \end{gathered}`

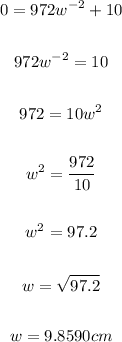
And the length is

`\begin{gathered} l=(162)/(9.8590) \\ \\ l=16.4316cm \end{gathered}`

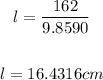
Therefore, to minimize the total area the length should be 16.4 cm and the width should be 9.9 cm.

Final Answer:

To minimize the total area the length should be 16.4 cm and the width should be 9.9 cm.