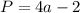A rectangle has an area of a^2 - a - 132. Findthe sides and then find the perimeter

Question

asked Dec 12, 2023 111k views

1 Answer

Cgat · Answer 1 · 2023-12-18T20:29:32+0000

Answer:

The sides are;

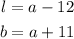
$\begin{gathered} l=a-12 \\ b=a+11 \end{gathered}$

The perimeter is;

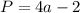
Step-by-step explanation:

The area of the rectangle is given as;

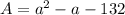
recall that area of a rectangle is length multiplied by breadth;

let us factorise the given equation;

$\begin{gathered} A=a^2-a-132 \\ A=a^2-12a+11a-132 \\ A=a(a-12)+11(a-12) \\ A=(a-12)(a+11) \end{gathered}$

Comparing the factorised equation to the formula for area;

$\begin{gathered} A=l* b=(a-12)(a+11) \\ l=a-12 \\ b=a+11 \end{gathered}$

The perimeter is given as;

substituting the values of l and b;

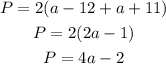
$\begin{gathered} P=2(a-12+a+11) \\ P=2(2a-1) \\ P=4a-2 \end{gathered}$

Therefore; the sides are;

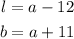
$\begin{gathered} l=a-12 \\ b=a+11 \end{gathered}$

The perimeter is;