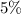Step-by-step explanation:
The total number of coin in the first bag is given below as
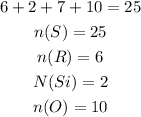
The probabaility of picking an orange ball from the first ba will b calcuated below as
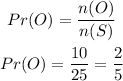
Step 2:
The total number of coin in the second bag is given below as
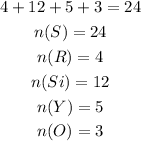
The probabaility of picking an orange ball from the second bag will be calcuated below as
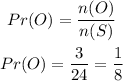
Hence,
The probabaility of picking an orange coin from both bags will be calculated below as
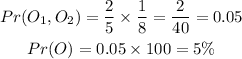
Hence,
The final answer is