Question

NUMBER 28 please:

Scientists studied the population of a species of bat in some caves in Missouri from 1983 to 2003. In 1983 there were 141,200 bats living in the caves. That number decreased by about 11% annually until 2003.

A. Identify the initial amount, the decay factor, and the decay rate

B. Write a function that models and number of that since 1983 then find the number of bats in 2003

Answer 1

a)

The initial amount is 141,200.

The decay factor is 0.89, and the decay rate is of 0.11 = 11%.

b)

The function is
`y(t) = 141200(0.89)^t`

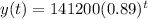
The number of bats in 2003 was of 13,729.

Explanation:

Exponential decay function:

An exponential decay function has the following format:

`y(t) = y(0)(1-r)^t`

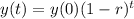
In which y(0) is the initial value, 1 - r is the decay factor and r is the decay rate, as a decimal.

A. Identify the initial amount, the decay factor, and the decay rate

In 1983 there were 141,200 bats living in the caves, which means that the initial amount is 141,200.

That number decreased by about 11% annually until 2003 means that the decay factor is 1 - 0.11 = 0.89 and the decay rate is 0.11 = 11%.

B. Write a function that models and number of that since 1983 then find the number of bats in 2003

With the data found in question A, we have that:

`y(t) = y(0)(1-r)^t`

`y(t) = 141200(1-0.11)^t`

`y(t) = 141200(0.89)^t`

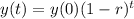
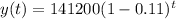
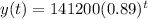
The function is
`y(t) = 141200(0.89)^t`

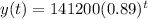
Number in 2003

2003 is 2003 - 1983 = 20 years after 1983, so this is y(20).

`y(20) = 141200(0.89)^(20) = 13729`

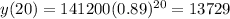
The number of bats in 2003 was of 13,729.