14) We have the function:
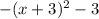
a) The parent function is the quadratic parent function f(x) = x^2.
b) We can graph the equation knowing that the vertex is at x=-3. The corresponding value for x=-3 is:
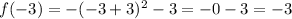
The vertex is (-3,-3).
As the sign in the quadratic term is neative, the parabola is concave down.
c) The transformation can be listed as:
- Reflection over the x-axis: this converts the original concave-up parabola into a concave-down parabola:
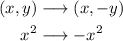
- Displacement 3 units to the left and 3 units down.
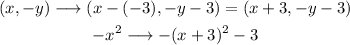
d) The domain is all the real numbers as there is no value of x for which f(x) is not defined.
The range can be defined as all the values of y that are equal or less than -3 (y<=-3).
15) We have the function:
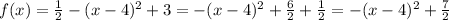
This case is similar to the previous one, but with a different displacement.
a) The parent function is the quadratic parent function f(x)=x^2.
b) The graph is:
The vertex is now (4,7/2).
The negative sign in the quadratic term tells us that the parabola is concave down.
c) The transformations are:
- Reflection over the x-axis.
- Displacement 4 units right and 7/2 units up.
d) The domain is all the real values and the range is all teh values of y that are less or equal than 7/2 (y<=7/2).