We can classify numbers elevated to an exponent as positive or negative depending on whether the exponent is an odd number or an even number.
When the number we have is a negative number, and we elevate that number to an exponent that is an even number, the result will be a positive number. For example:

And when the number we have is a negative number (such as the case of -7) and we elevate that number to an exponent that is an odd number (such as the case of 2015), the result will be a negative number.
We can explain this result using smaller numbers, for example:
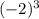
We can express this as a multiplication of three times -2:
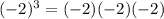
And the result will be negative:
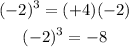
This will always be the case when we have a negative number elevated to an odd power.
Answer: (-7)^2015 is a negative number because the exponent is an odd number.