1 Answer

Ask a Question

DudeDoesThings · Answer 1 · 2023-12-27T17:38:56+0000

ANSWER

1.52 x 10⁶ m/s²

Step-by-step explanation

Free-body diagram,

The net force on the satellite is,

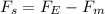
Where Fe is the force of attraction between the satellite and the Earth and Fm is the force of attraction between the satellite and the moon.

First, with the data from #2, we have to find the distance between the Earth and the Moon, using Newton's law of universal gravitation,

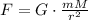
$F=G\cdot(mM)/(r^2)$

Solve for r,

$r=\sqrt[]{G\cdot(Mm)/(F)}\approx3.83*10^8m$

Now, the attraction force between the satellite and the Earth is,

$F_E=G(Mm)/(r^2)=6.67*10^(-11)\frac{m^3}{\operatorname{kg}s^2}\cdot\frac{5.98*10^(24)\operatorname{kg}\cdot1200\operatorname{kg}}{((2)/(3)\cdot3.83*10^8m)^2}\approx1.87*10^9N$

And between the satellite and the Moon,

$F_m=G(Mm)/(r^2)=6.67*10^(-11)\frac{m^3}{\operatorname{kg}s^2}\cdot\frac{7.34*10^(22)\operatorname{kg}\cdot1200\operatorname{kg}}{((1)/(3)\cdot3.83*10^8m)^2}\approx4.6*10^7N$

The net gravitational force the satellite experiences is,

$F=F_E-F_m\approx1.824*10^9N$

The gravitational field constant is the quotient between the weight of the object and its mass,

$g=(F)/(m)=\frac{1.824*10^9N}{1200\operatorname{kg}}=1.52*10^6m/s^2$

Use an FBD and data from #2, calculate the net force acting on a satellite at 2/3 the-example-1

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions