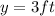Answer:
A.
Solving the equation for the leg y will give;

B.
The length of the leg y is;
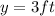
Step-by-step explanation:
Given that the perimeter of this trapezoid is given by;
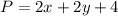
A.
Solving for y, we have;
solving the equation for the leg y will give;

B.
If the perimeter of the figure is 26 feet and the shorter base, x, is 8 feet;

Substituting;
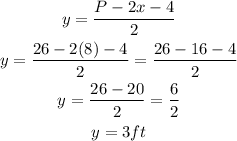
Therefore, the length of the leg y is;