Question

Vector A has a magnitude of 3.0 units and makes an angle of −90.0° with the positive x-axis. Vector B has a magnitude of 4.0 units and makes an angle of −120° with the positive x-axis. What is the direction of the vector sum A + B relative to the positive x-axis .

Answer 1

Given data:

* The magnitude of the vector A is 3 units.

* The magnitude of the vector B is 4 units.

* The direction of vector A with the positive x-axis is - 90 degree.

* The direction of the vector B with the positive x-axis is - 120 degree.

Solution:

The diagrammatic representation of the given vectors is,

The resultant horizontal components of both the vectors is,

`\begin{gathered} X=3\cos (90^(\circ))+4\cos (120^(\circ)) \\ X=0+4\cos (90^(\circ)+30^(\circ)) \\ X=-4\sin (30^(\circ)) \\ X=-2\text{ units} \end{gathered}`

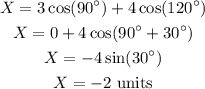
The resultant vertical component of both the vectors is,

`\begin{gathered} Y=-3-4\cos (120^(\circ)-90^(\circ)) \\ Y=-3-4\cos (30^(\circ)) \\ Y=-6.46\text{ units} \end{gathered}`

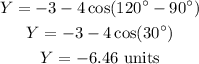
The direction of the resultant of both the vectors is,

`\tan (\theta)=(Y)/(X)`

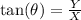
Substituting the known values,

`\begin{gathered} \tan (\theta)=(-6.46)/(-2) \\ \tan (\theta)=3.23 \\ \theta=-107.2^(\circ) \end{gathered}`

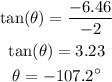
Here negative sign indicates that resultant vector is present in third quadrant and the angle of resultant from the positive x-axis is measured in anticlockwise direction.

Thus, the direction of sum A+B (or resultant of vector A and B) is -107.2 degree or approx -107 degree.

Hence, option A is the correct answer.