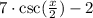Question

I need help with this practice I am having trouble solving it The subject is trigonometry from my ACT prep guide

Answer 1

Remember that the range of the parent function csc(x) is:

`(-\infty,-1\rbrack\cup\lbrack1,\infty)`

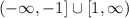
If we apply a vertical stretch by a factor k, the function becomes:

`\csc (x)\rightarrow k\cdot\csc (x)`

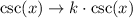
And the range becomes:

`(-\infty,-k\rbrack\cup\lbrack k,\infty)`

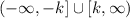
If we then apply a vertical shift by c units, the function becomes:

`k\cdot\csc (x)\rightarrow k\cdot\csc (x)+c`

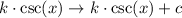
And the range becomes:

`(-\infty,-k+c\rbrack\cup\lbrack k+c,\infty)`

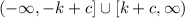
Then, we can identify the endpoints of the interval with the given range:

`(-\infty,-9\rbrack\cup\lbrack5,\infty)`

So:

`\begin{gathered} -k+c=-9 \\ k+c=5 \end{gathered}`

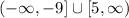
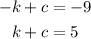
Solving the system of equations yields c=-2 and k=7. Replace these values into the transformed function:

`k\cdot\csc (x)+c=7\csc (x)-2`

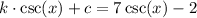
On the other hand, two consecutive asymptotes of the parent function are x=0 and x=π. Apply a horizontal stretch by 2 units to get the equation of the described cosecant function:

`7\csc (x)-2\rightarrow7\csc ((x)/(2))-2`

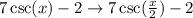
Therefore, the equation of the described cosecant function is:

`7\cdot\csc ((x)/(2))-2`