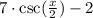Remember that the range of the parent function csc(x) is:
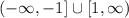
If we apply a vertical stretch by a factor k, the function becomes:
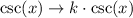
And the range becomes:
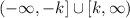
If we then apply a vertical shift by c units, the function becomes:
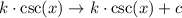
And the range becomes:
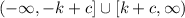
Then, we can identify the endpoints of the interval with the given range:
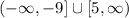
So:
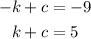
Solving the system of equations yields c=-2 and k=7. Replace these values into the transformed function:
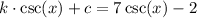
On the other hand, two consecutive asymptotes of the parent function are x=0 and x=π. Apply a horizontal stretch by 2 units to get the equation of the described cosecant function:
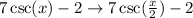
Therefore, the equation of the described cosecant function is: