Question

At witch values of x does the function f(x) have a vertical asymptote check all that apply

Answer 1

In this problem, we are seeking the vertical asymptotes. To find them, we need to find restricted values from the denominator of the rational expression.

Recall that we are not allowed to divide by 0 in any fraction or rational expression. We will use the factored form to find those values of x that restrict our denominator.

Normally, the first step is to completely factor the denominator. But the good news is that's already been completed for us:

`F(x)=(1)/(7(x+2)(x+3))`

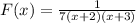
We will use the factors to find the restricted values by setting them equal to zero. Let's begin with x+2:

`\begin{gathered} x+2=0 \\ x+2-1=0-2 \\ x=-2 \end{gathered}`

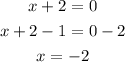
So, one of our vertical asymptotes is x= -2.

Following those procedures, we will use x + 3:

`\begin{gathered} x+3=0 \\ x+3-2=0-3 \\ x=-3 \end{gathered}`

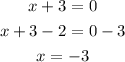
The second vertical asymptote is x= -3.

The correct options in your question are A and D.