We are given that the triangles ABC and QPR are similar.
Recall the properties of similar triangles,
• Corresponding angles are equal.
,
• Corresponding sides are in the same ratio.
Let us first identify the corresponding sides
Side AB = Side QP
Side BC = Side RP
Side AC = Side QR
Now let us find the missing side length RP using the ratio of corresponding sides.
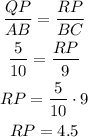
So, the length of the side RP is 4.5 hence the 2nd option is correct.
Now let us check the corresponding angles.
m∠R = m∠C
m∠Q = m∠A
m∠P = m∠B
From the figure, we see that
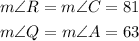
Hence the 1st option and the 3rd option are correct.
Recall that the sum of the interior angles of a triangle is equal to 180°
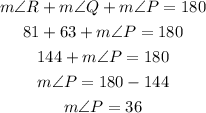
Hence, the last option is incorrect since the m∠P is 36° (not 81°)
Therefore, the correct options are 1st, 2nd, and 3rd only.