Question

A newbom child receives a $6,000 gift toward a college education from her grandparents. How much will the $6,000 be worth in 19 years it it is invested at 7.8%compounded quarterly?

Answer 1

The total amount for a compound interest is given by the formula:

`A=P(1+(r)/(n))^(nt)`

where P is the principal (the initial investment), r is the interest rate in decimal form, n is the number of times the amount is compounded in a given time t and t is the time of investment.

In this case the principal is $6000, the interest rate in decimal form is 0.078, since the amoun is compounded quarterly then n=4, and the time of investment is 19. Plugging this in the formula we have:

`\begin{gathered} A=6000(1+(0.078)/(4))^(4\cdot19) \\ A=26036.39 \end{gathered}`

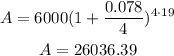
Therefore, the total amount after 19 years is $26,036.39