Question

use Newton's law of cooling to solve the problem Note: this is an algebra 2 problem. However, after 4 math tutors from here, they all couldnt answer and claimed its a physics problem. Maybe a physics tutor can helo? if needed, I can send a practice problem which is similar. we did it in class

Answer 1

Newton's law of cooling relates the temperature of an object with the time. This law is the following:

`T=(T_0-T_r)e^(rt)+T_r`

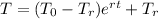
Where:

`\begin{gathered} T=\text{ temperature at time`

Since we are asked to determien time we need to solve for "t". To do that we will subtract the temperature of the surrounding from both sides:

`T-T_r=(T_0-T_r)e^(-rt)`

Now, we divide by the factor multiplying "e":

`(T-T_r)/(T_0-T_r)=e^(-rt)`

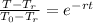
Now, we use natural logarithm on both sides:

`\ln ((T-T_r)/(T_0-T_r))=\ln (e^(-rt))`

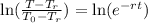
Now, we use the following property of logarithms on the right side:

`\ln e^x=x`

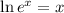
This means that we can lower the exponent, like this:

`\ln ((T-T_r)/(T_0-T_r))=-rt`

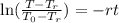
Now, we divide both sides by "-r":

`-(1)/(r)\ln ((T-T_r)/(T_0-T_r))=t`

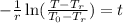
Now, we substitute the values:

`-(1)/(0.067)\ln ((100F-72F)/(180F-72F))=t`

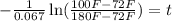
Solving the operations:

`20.15\min =t`

Therefore, the time to wait is 20.15 minutes.