Given the following expression:
![\frac{(16 \sqrt[]{x})^2 }{y^(-1)}](https://img.qammunity.org/2023/formulas/mathematics/college/illvd4xf840hxp41qwd2ctajk7zlmsz59q.png)
You need to remember the Rules of Exponents shown below:
- Negative Exponent Rule:

Where "b" is the base and "n" is the exponent.
- Fractional Exponent Rule:
![b^{(m)/(n)}=\sqrt[n]{b^m}](https://img.qammunity.org/2023/formulas/mathematics/college/48tckl409vuuy53uvo4fj36tgnk5bczh38.png)
- Power of a Product Rule:
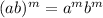
In this case, knowing the rules shown above, you can simplify the expression as follows:
1. Apply the Power of a Product Rule in the numerator:
![=\frac{(16)^2(\sqrt[]{x})^2}{y^(-1)}=\frac{256^{}(\sqrt[]{x})^2}{y^(-1)}](https://img.qammunity.org/2023/formulas/mathematics/college/otslf9nlz2rovk70na6zmqso65ungymc5f.png)
2. Apply the Fractional Exponent Rule to simplify the square root:
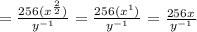
3. Finally, apply the Negative Exponent Rule:
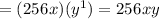
Therefore, the answers are:
- Expression simplified:
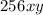
- Rules of Exponents used to simplify it:
1. Power of a Product Rule:
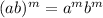
2. Fractional Exponent Rule:
![b^{(m)/(n)}=\sqrt[n]{b^m}](https://img.qammunity.org/2023/formulas/mathematics/college/48tckl409vuuy53uvo4fj36tgnk5bczh38.png)
3. Negative Exponent Rule:
