The equation thatmodels the movement of the objet is:
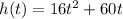
where h(t) is equal to the hight and t is the time, so we can replace h(t)=36 so:
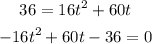
now we can use the cuadratic function to find the values of t so:
![\begin{gathered} \frac{-b\pm\sqrt[]{b^2-4(a)(c)}}{2a} \\ a=-16 \\ b=60 \\ c=-36 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hsu669vv2n63vnhaobx828zw7ptf2uj8vh.png)
So the equation become:
![\frac{-60\pm\sqrt[]{60^2-4(-16)(-36)}}{2(-16)}](https://img.qammunity.org/2023/formulas/mathematics/college/3lo6fu2wse2jz8uiximg248fs3hz62lvdi.png)
Now we operate so:
![\begin{gathered} \frac{-60\pm\sqrt[]{3600-2304}}{-32} \\ \frac{-60\pm\sqrt[]{1296}}{-32} \\ (-60\pm36)/(-32) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bu5j31jjsl72a3yqw4wtmq627jch04i3bj.png)
Now we solve bout solutions:
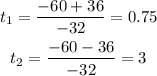
So he will reach a hight of 36 feets at 0.75 seconds and a time of 3 seconds because the first time is when his is going up and the second time is we he is falling back to the grownd.