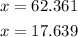1)
To find out the profit we must subtract the expense from the income. We have both functions, we know that the expense is
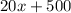
And the income
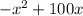
The profit will be (income - expense), therefore:

The profit is given by
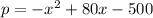
2)
Now we must discover the ticket price they would break even, the break-even point happens when the income and the expense are the same, then (expense = income)
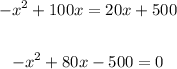
See that, it's the same as the profit, we knew that the profit was
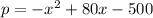
The break-even happens when p = 0.
Now we must solve that quadratic function
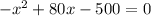
Using the quadratic formula
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Where a = -1, b = 80, c = -500.
![\begin{gathered} x=\frac{-80\pm\sqrt[]{80^2-4\cdot(-1)\cdot(-500)}}{2\cdot(-1)} \\ \\ x=\frac{-80\pm\sqrt[]{4400}}{-2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/lh7xck9e0g1gd147w11vfiq90ap1db6xgj.png)
If we simplify the expression
![\begin{gathered} x=\frac{-80\pm20\, \, \sqrt[]{11}}{-2} \\ \\ x=40\pm10\, \, \sqrt[]{11} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/dmvmlpjyte9i03d6k2tg48vbabnhu3jnpc.png)
Therefore they would break-even at
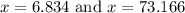
3)
The max profit will be the vertex of the profit function (parabola), the vertex of a parabola is
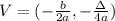
Here, the values of "x" is the ticket price and the "y" values are the profit.
Using the x coordinate to find out the vertex ticket price we have:

Remember that a = -1, b = 80, c = -500, therefore
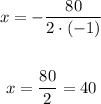
They reach the maximum profit when the ticket price is $40
4)
To find out the maximum profit we can use x = 40 in the profit formula
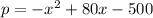
Put x = 40
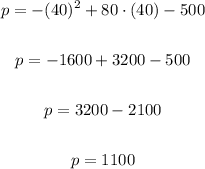
The maximum profit is $1100
5)
If we want a determined profit and find the ticket price, we must take the profit function:
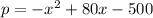
And solve that function for "x", which is the same to discover the ticket price for a generic profit.
So, we will solve the quadratic for a generic value of p:
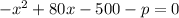
Now, we have a = -1, b = 80, c = -500 - p.
Using again the quadratic formula, we can solve it for x
![\begin{gathered} x=\frac{-80\pm\sqrt[]{80^2-4\cdot(-1)\cdot(-500-p)}}{2\cdot(-1)} \\ \\ x=\frac{-80\pm\sqrt[]{4400-4p}}{-2} \\ \\ x=\frac{-80\pm2\, \sqrt[]{1100-p}}{-2} \\ \\ x=40\pm\, \sqrt[]{1100-p} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/jugjpsegipem3fdoebez4vdqox5qh2u483.png)
Therefore, given a profit value, the ticket price will be
![x=40+\sqrt[]{1100-p}\text{ or }x=40-\sqrt[]{1100-p}](https://img.qammunity.org/2023/formulas/mathematics/high-school/togejkbybqy2zvcrfgyfyh6apg2jjef9p3.png)
Examples:
Let's suppose that the profit is $600, we just have to put p = 600 and simplify the expression, some of them may be hard to find by hand so use a calculator. The "strange" part here is: there are two values that the ticket can be
![x=40+\sqrt[]{1100-p}\text{ or }x=40-\sqrt[]{1100-p}](https://img.qammunity.org/2023/formulas/mathematics/high-school/togejkbybqy2zvcrfgyfyh6apg2jjef9p3.png)
Let's put p = 600 and solve
![\begin{gathered} x=40+\sqrt[]{1100-p}\text{ or }x=40-\sqrt[]{1100-p} \\ x=40+\sqrt[]{1100-600}\text{ or }x=40-\sqrt[]{1100-600} \\ x=62.360\text{ or }x=17.639 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/wevva8l2ihzwfyjl8v75sgdf7h78oi9szu.png)
Therefore for p = 600 the ticket price and be 62.360 or 17.639.
Let's solve it using the quadratic function to check if our result is correct:
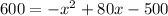
We must have zero on one side, then
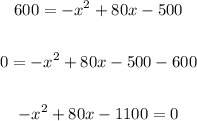
And now we solve using the quadratic formula
![\begin{gathered} x=\frac{-80\pm\sqrt[]{80^2-4\cdot(-1)\cdot(-1100)}}{2\cdot(-1)} \\ \\ x=\frac{-80\pm\sqrt[]{2000}}{-2} \\ \\ x=40\pm10\, \, \sqrt[]{5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/2v5p0i9pxu9dt7qfs5998c8fncvcqa7cey.png)
If you put that result in decimal we get