Answer:
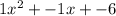
Explanation:
Fill in the left side of the grid with the first factor, x + 2 , and fill in the top of the grid with the second factor, x - 3 . Then complete the inside of the grid using the outside tiles as the length and the width of the inside area.
Next cancel out any zero pairs. In this model, two pairs of x and -x tiles can be canceled out.
So the expression (x + 2)( x - 3) is rewritten as
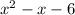 .
.