Question

I don’t know how to solve this question just need some quick help

Answer 1

To factor the expression over the complex numbers, let's fin its roots, then we will be able to write it in the generic form of a factored polynomial as follows:

`(x-a)(x-b)`

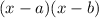
Where a and b stand for the roots of the polynomial.

`\begin{gathered} x^2+50=0\to x^2=-50 \\ \to x_(1,2)=\pm\sqrt[]{-50} \\ x_1=i\sqrt[]{50} \\ x_2=-i\sqrt[]{50} \end{gathered}`

From this, we can rewrite the polynomial as follows:

`x^2+50=(x+i\sqrt[]{50})(x-i\sqrt[]{50})`