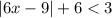
When you have a absolute value in a inequality, to solve:
1. Leave the absolute value in one side of the inequality sing and the other terms in the other side:
-Substract 6 in both sides of the inequatily:
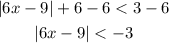
2. As the abosule value is less than a negative number you have no solution for the system, you can see it by following the next steps:
-Write the inequality as two inequalities, one with the sing < and the other with the sing >:
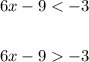
Solve the first inequality:
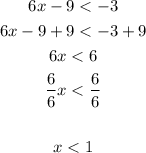
Solve the secodn inequality:

If you combine those solutions you get:
[tex]1As you can see the system has no solution as x cannot be less than 1 and greather than 1 at the same time.
Then, the inequality doesn't have solution