Question

A car traveling at 13.6 meters per second crashes into a barrier and stops in 0.321 meters. How many times the weight of the child is this force? The force exerted on the child is -6110 N. The mass of child is 21.2 kg.

Answer 1

Given data:

* The velocity of the car is 13.6 m/s.

* The car stops in 0.321 m.

* The force exerted on the child of mass 21.2 kg is -6110 N.

* The mass of the child is 21.2 kg.

Solution:

The weight of the child is,

`W=mg`

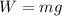
where m is the mass of the child, and g is the acceleration due to gravity,

Substituting the known values,

`\begin{gathered} W=21.2*9.8 \\ W=207.76\text{ N} \end{gathered}`

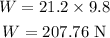
By dividing the force exerted on the child with the weight of the child,

`\begin{gathered} (F)/(W)=(6110)/(207.76) \\ (F)/(W)=29.4 \\ F=29.4* W \end{gathered}`

Thus, the force is 29.4 times the weight of the child.