To answer this question we will use the following formula to compute the volume of a cylinder:
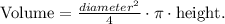
Therefore, the volume of container A is:
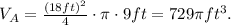
The volume of container B is:
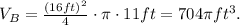
Now, after pumping the water, the percent of container A that is empty is:
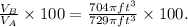
Simplifying the above result we get:
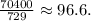
Answer: 96.6%