Question

Jim began a 200 mile bike trip to build up stamina for a triathlete competition. Unfortunately, his bike chain broke, so he finished the trip walking. The whole trip took 8 hours. If Jim walks at a rate of 3 miles per hour and rides at 35 miles per hour, find the amount of time he spent on the bicycle

Answer 1

That is a simple question to solve.

First, let's consider the whole trip = 8 hours. If, between this 8 hours, we have x hours travelled by bicycle and y hours travelled on foot, we have:

`\text{wholetrip}_{\text{hours}}=\text{bicycle}_{\text{hours}}+\text{walking}_{\text{hours}}`

Once:

`\begin{gathered} \text{wholetrip}_{\text{hours}}=8\text{ hours} \\ \text{bicycle}_{\text{hours}}=\frac{x}{\text{bicycle}_{\text{miles}/h}} \\ \text{walking}_{\text{hours}}=\frac{(200-x)}{\text{walking}_{\text{miles}/h}} \end{gathered}`

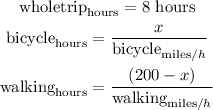
So, we have:

`\begin{gathered} 8_{}=(x)/(35)_{}+((200-x))/(3) \\ 8_{}=(3x+7000-35x)/(105) \\ 840-7000=3x-35x \\ x=(6160)/(32) \\ x=192.5miles \end{gathered}`

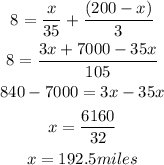
Where x is the number of miles spent by bicycle.

Now, for y (number of miles spent walking) we have:

`\begin{gathered} y=200-192.5 \\ y=7.5miles \end{gathered}`

Now we can calculate the amount of time spent walking and on the bicycle as follows:

`\begin{gathered} \text{walking}_{\text{hours}}=((200-192.5))/(3) \\ \text{walking}_{\text{hours}}=2.5h \end{gathered}`

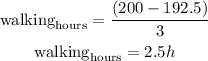
and,

`\begin{gathered} \text{bicycle}_{\text{hours}}=(192.5)/(35) \\ \text{bicycle}_{\text{hours}}=5.5h \end{gathered}`

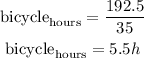
So, the final answer is: Jim spent 5.5 hours on the bicycle.