If you have two lines, for example:

with slope "m"
and
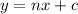
with slope "n"
That are perpendicular, the relationship between the slopes is that one is the inverse negative of the others, symbolically:

So the first step is to use the known points of one of the lines to calculate the slope using the formula:
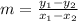
For (5,7) and (10,3)
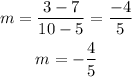
Now that you have determined the value of the slope, you can determine the slope of a line perpendicular to it as:
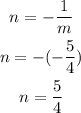
The slope of the perpendicular line to one that passes through points (5,7) and (10,3) is 5/4