Question

Find the sum of the infinite geometric series 1+ 0.2+0.04 +0.008 +OA. 1.25OB.2OC the series divergesOD.3Reset Selection

Answer 1

Given: The series below

`1+0.2+0.04+0.008+...`

To Determine: The sum of the infinite geometric series

Solution

Let us determine the common ratio

For a geometric series with terms a1, a2, a3, ... as below

`\begin{gathered} a_1+a_2+a_3+...+a_(n-1)+a_n \\ r=(a_2)/(a_1)=(a_3)/(a_2)=(a_n)/(a_(n-1)) \end{gathered}`

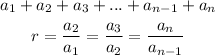
Let us apply the above to the given question

`\begin{gathered} ratio(r)=(0.2)/(1)=(0.04)/(0.2)=(0.008)/(0.04)=0.2 \\ r=0.2 \end{gathered}`

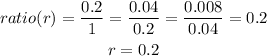
The first term a is 1

`a=1`

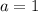
Please note the below

Since the common ratio r is less than 1, the series converges, the sum to inifinity would be

`\begin{gathered} S_(\infty)=(a)/(1-r) \\ a=1 \\ r=0.2 \\ S_(\infty)=(1)/(1-0.2) \\ S_(\infty)=(1)/(0.8) \\ S_(\infty)=(10)/(8) \\ S_(\infty)=1.25 \end{gathered}`

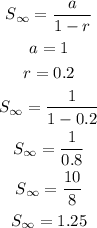
Hence, the sum of the infinite geometric series is 1.25, OPTION A