Answer
The variation constant is 108
The equation of variation is y = 108/x
Step-by-step explanation
y varies inversely to x implies:
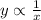
So, introducing a constant, we have
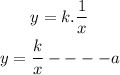
Substitute y = 12 and x = 9 into (a)
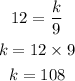
Therefore the variation constant = 108
To find the equation of variation, substitute k = 108 into (a)
